1ª Série - volume 1 2022

GABARITO B
RESOLUÇÃO
O percentual de doadores desse país é de 1,9%. Analisando a tabela, vimos que o percentual de doadores menores ou iguais a 1,9% são Nordeste, Norte e Sudeste.

GABARITO B
RESOLUÇÃO
Basta perceber que o ponto mais alto no gráfico é onde temos o maior percentual de promoções das regiões. Olhando para cada região respectivamente podemos concluir que a resposta correta é letra B.

GABARITO D
RESOLUÇÃO
A população economicamente ativa em 05/09 é de: 23.020.000.
A taxa de crescimento entre 05/09 e 06/09 é: 4%.
Então o número de pessoas economicamente ativas em 06/09 será de:
104% . 23.020.000 = 23.940.800

GABARITO D
RESOLUÇÃO
Para calcular a taxa média da variação da emissão de dióxido de carbono (em ppm), soma-se todas as variações e divide-se pelo número de variações:2,30 − 2,14 + 2,46 − 2,30 + 2,64 − 2,46 + 2,83 − 2,64 + 3,03 − 2,83 + 3,25 − 3,03 + 3,48 − 3,25 + 3,73 − 3,48 + (4,00 − 3,73) 9 = 0,16 + 0,16 + 0,18 + 0,19 + 0,20 + 0,22 + 0,23 + 0,25 + 0,279 = 1,869 = 0,207 (aproximadamente). Como a variação da produção (em toneladas) foi a mesma a cada intervalo, sua média será igual a este próprio valor 0,1. A taxa média de variação entre a emissão de dióxido de carbono (em ppm) e a produção (em toneladas) é calculada através da divisão desses dois resultados: 0,207/0,1 = 2,07, portanto superior a 1,5 e inferior a 2,8.

GABARITO D
RESOLUÇÃO
Para realizar o cálculo do IGP-M fazemos:
Mês de Janeiro
JAN (IGP-M) = 0,52*10 + 0,100*30 + 0,51*60/(10+30+60)
JAN (IGP-M) = 65,8/100
JAN (IGP-M) = 0,658
Mês de Fevereiro
FEV (IGP-M) = 0,35*10 + 0,88*30 + 1,42*60/(10+30+60)
FEV (IGP-M) = 115,1/100
FEV (IGP-M) = 1,15
Mês de Março
MAR (IGP-M) = 0,45*10 + 0,83*30 + 1,07*60/(10+30+60)
MAR (IGP-M) = 93,60/100
MAR (IGP-M) = 0,936
Como você pode ver, o maior resultado para o primeiro trimestre foi do mês de fevereiro em que o IGP-M foi de 1,15;

GABARITO E
RESOLUÇÃO
Capacidade da van = 15
Quantidade dos faltosos = x
Quantidade dos que compareceram = 15 – x
Quem compareceu paga 2 reais a maior por cada um que faltou = (15 – x)(2x)
V(x) = [(15-x)60] + [(15-x)(2x)]
V(x) = 900 – 60x + 30x – 2x²
V(x) = 900 – 30x – 2x²

GABARITO A
RESOLUÇÃO
O número de desempregados em março de 2010, na região metropolitana de Porto Alegre, foi de 9,8% de 250 000 e portanto: 9,8% . 250 000 = 24 500

GABARITO E
RESOLUÇÃO
De acordo com a tabela, os estudantes passam 5 horas por dia estudando em cada um dos 5 dias da semana e 1 hora a cada dia no fim de semana. Assim estudam 5 . 5 + 1 . 2 = 27 horas por semana.

GABARITO A
RESOLUÇÃO
Calcula-se o ganho por ação de cada investidor através da diferença entre o valor da venda e o da compra. Os valores de compra e venda são retirados do gráfico de acordo com a hora em que foram efetuados. Aquele cujo valor for maior é o que fez o melhor negócio, uma vez que todos venderam a mesma quantidade de ações.
Investidor 1: 460 – 150 = 310
Investidor 2: 200 – 150 = 50
Investidor 3: 460 – 380 = 80
Investidor 4: 100 – 460 = -360 (prejuízo de R$ 360,00)
Investidor 5: 150 – 50 = 100
O maior valor é 310 reais, obtido pelo investidor 1.

GABARITO D
RESOLUÇÃO
Sabendo que a pesquisa ouviu 1165 pessoas, segue que o resultado pedido é:
0,59.1165 = 687

GABARITO E
RESOLUÇÃO
As taxas mostradas no gráfico estão em percentuais. O desemprego em dezembro de 2012 é de 2,2/2 = 1,1 porque é a metade do desemprego de junho de 2012. O desemprego total é de 9,0 porque é igual ao de dezembro de 2011. A taxa de desemprego aberto em dezembro de 2012 será de 9 – 1,1 = 7,9.

GABARITO D
RESOLUÇÃO
Primeira figura: Para menores temperaturas (motor frio) e em pista em aclive a emissão de CO é maior.
Segunda figura: Para baixas velocidades médias e em pista em aclive, a emissão de CO é maior.

GABARITO B
RESOLUÇÃO
Como ele disse que é uma função quadrática, então:
Q = At² + Bt + C ;
1 = c ;
T = 1
4 = a + b + 1
a + b = 3 ;
T = 2 ;
6 = 4a + 2b + 1 ;
A + b = 3 = A = 3 - b
4a + 2b = 5 (3-b) + 2b = 5 ;
12 - 4b + 2b = 5
+ 2b = +7
B = 7/2 ;
A = 3 - 7/2
A = 6/2 - 7/2
A = -1/2
Finalizando então:
A = -t²/2 + 7/2t + 1 ;
Q = -9/2 + 21/2 + 2/2 ;
Q = 7.

GABARITO C
RESOLUÇÃO
Fórmula: An= A1+ (n-1) * R
Observa-se que o aumento de médicos é a cada 5 ano na qual a razão pela diferença é 25 , por exemplo, 162-137, esse é o termo r.
Se separarmos todos os anos serão ( 1980,1985,1995,2000,2005...2040) na qual são 13 termos ( An)
O primeiro termo é o 137 ( a1)
Agora é só jogar na fórmula :
An= A1+ (n-1) * R
A13= 137 + ( 13-1) * 25
A13= 137 + 12*25
A13= 137+300
A13= 437

GABARITO E
RESOLUÇÃO
Na interpretação do gráfico do modelo predador-presa devemos buscar o intervalo em que f(x) está abaixo de g(x) e h(x). Ou seja, para um mesmo valor de x a curva f deve estar com o valor no eixo y menor que g e h.
Podemos observar no gráfico que de 0 a C, f(x) é maior que h(x), e de 0 a B f(c) será maior que g(x). Logo, apenas para x entre C e E teremos f(x) menor que g(x) e h(x) simultaneamente.
Sendo assim, o maior intervalo que a resposta funcional f(x) é menor que as outras respostas será (C ; E).

GABARITO D
RESOLUÇÃO
h = 30 cm ( momento em que a planta é colocada à venda)
h = 40 cm ( momento em que atingirá a altura máxima)
Quanto tempo leva entre um momento e o outro?
Para descobrir, devemos resolver duas equações logarítmicas.
30 = 5·log2 (t + 1) 40 = 5·log2 (t + 1)
6 = log2 (t + 1) 8 = log2 (t + 1)
26 = t+1 28 = t+1
64 = t + 1 256 = t + 1
t = 63 t = 255
Finalmente, basta diminuir: 255 - 63 = 192 dias.

GABARITO D
RESOLUÇÃO

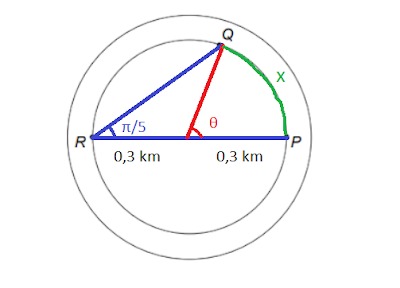
O objetivo da questão é calcular o comprimento do arco PQ que estamos chamando de x.
Para calcular o comprimento deste arco, devemos utilizar a seguinte relação:
θ = x / 0,3
x = 0,3 . θ
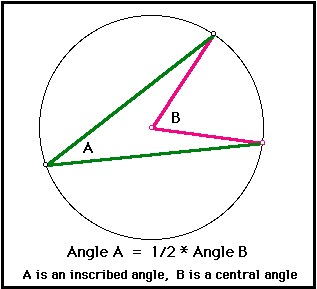
O valor de θ é duas vezes o ângulo π/5, devido a regra do ângulo inscrito em uma circunferência.

Finalmente temos que x = 0,3 . 2 . π/5 = 0,12 . π

GABARITO B
RESOLUÇÃO
Comprimento da semicircunferência entre PN e PS: 20.016 km
Latitude percorrida no trajeto do navio: 30°
Com essas anotações notamos que o trajeto percorrido, está circunciso no comprimento PN e PS, e a metade desse comprimento é igual ao comprimento mais aproximado dos quilômetros percorridos pelo navio, sendo igual a :
20016 ÷ 2 =10008 km.
Esse comprimento de 10008 km faz um angulo reto com a linha do equador, um ângulo de 90° . O comprimento do navio está circunciso nesse comprimento, sendo assim, podemos estabelecer a relação:
90° ⇔ 10008 km
30° ⇔ x
multiplicando cruzado temos:
= 3336 km.

GABARITO E
RESOLUÇÃO
A esposa utiliza uma média de 30 minutos por mês.
Temos que analisar o gráfico e verificar qual o plano oferece o menor valor de conta para 30 minutos de uso por mês.
No plano A, a esposa pagaria aproximadamente 45 reais por mês.
No plano B ela pagaria um pouco mais de 45 reais por mês.
No plano C, ela pagaria menos de 45 reais por mês.

Logo, o plano C apresenta o melhor custo mensal para a esposa.
O marido utiliza uma média de 90 minutos por mês.
Temos que analisar o gráfico e verificar qual o plano oferece o menor valor de conta para 90 minutos de uso por mês.
No plano A, o marido pagaria aproximadamente 90 reais por mês.
No plano B ele pagaria menos de 90 reais por mês.
No plano C, ele pagaria mais de 100 reais por mês.
Logo, o plano B apresenta o melhor custo mensal para o marido.

GABARITO B
RESOLUÇÃO
Observe, no gráfico, a marcação de cinco pontos.
No ponto 1, o carro ultrapassou a velocidade máxima permitida e o dispositivo alertou o motorista.
No ponto 2, o carro está retornando à velocidade máxima permitida. Então, o dispositivo não tocou.
No ponto 3, o carro atinge a velocidade máxima permitida, mas não a ultrapassa. Logo, o dispositivo não tocou.
No ponto 4, o carro volta a ultrapassar a velocidade máxima permitida, então o dispositivo alertou o motorista.
No ponto 5, o carro está retornando à velocidade máxima permitida. Então, o dispositivo não tocou.
Portanto, o dispositivo alertou o motorista apenas nos pontos 1 e 4.
Ou seja, só tocou 2 vezes.

GABARITO D
RESOLUÇÃO
Analisando o gráfico, verifica-se que no tempo t1, no tempo t4 e no tempo t6, a intensidade sonora no ambiente ULTRAPASSOU o limite de 65 decibéis; portanto, nestes instantes, os funcionários precisaram de colocar a proteção de ouvidos.
Observe que no tempo t3 a intensidade sonora atingiu o limite de 65 decibéis, porém, não o ultrapassou.
Portanto, os protetores de ouvidos foram colocados 3 vezes.

GABARITO A
RESOLUÇÃO
Lembrando que uma equação do segundo grau possui a seguinte forma:
y = ax² +bx + c
Como a concavidade da parábola é para baixo, então o coeficiente "a" é negativo. Então, podemos eliminar as alternativas b) e c)
Na equação do segundo grau temos duas propriedades importantes chamadas Soma e Produto das raízes.
Temos que a soma é igual a S = x + x” = -b/a e o produto é igual a P = x’.x” = c/a .
Da figura 2 temos que x' = -5 e x'' = 5. E temos também que c = 10. Logo.
S = -5 + 5 = 0
-b/a = 0
b = 0
P = -5.5 = -25
c/a = -25
10/a = -25
a = -2/5
Portanto, a equação que descreve a parábola da figura 2 é y = -2x²/5 + 10

GABARITO D
RESOLUÇÃO
Ele disse que a cada real cobrado diminui 10 clientes dos 200. Então vamos considerar essa quantidade de reajuste como x. Então ficaria assim
(10+x) . ( 200- 10x)
Então, multiplicando os termos, teremos:
2000 + 100x – 10x²
Fazendo a fórmula do x do vértice iremos descobrir o quanto será acrescido
-b/2a
Então ficará:
-100/2.(-10)
-100/-20
5
Assim, 5=x. Agora basta adicionarmos esse valor ao já existente para ter o novo preço: 10 + 5 = 15

GABARITO B
RESOLUÇÃO
Após 8 anos, os bens estarão reduzidos a 100 – 80 = 20% dos seus valores iniciais. Portanto,
0,2 . (1200 – 900) = 60.

GABARITO D
RESOLUÇÃO
Repare que 2 horas após a sessão de treinamento, a liberação de GH em todas as intensidades é a mesma. Logo apenas nas medições feitas logo após e 1 hora após a sessão de treinamento, a liberação de GH na corrente sanguínea em uma sessão de intensidade máxima foi maior do que a liberação de GH ocorrida nas demais intensidades.

GABARITO C
RESOLUÇÃO
A função de depreciação é dada por f(t) = b.a^t, então precisamos encontrar os valores de a e b, para isso, consideramos dois pontos conhecidos e resolvemos o sistema:
60000 = b.a^0
b = 60000
54000 = b.a^1
a = 54000/60000
a = 0,9
Logo, a função é f(t) = 60000.0,9^t. Com isso, substituindo t = 2, temos o valor do automóvel após dois anos:
f(2) = 60000.0,9²
f(2) = R$48.600,00

GABARITO D
RESOLUÇÃO
Se o time fez 77 pontos em 38 jogos, e como as derrotas não somam e nem diminuem a pontuação da equipe, então cada vitória são ganhos 3 pontos e a cada empate é ganho 1 ponto. Assim, temos que a quantidade de pontos do time em 2013 será:
P = 3.V + 1. E – 2.D

GABARITO C
RESOLUÇÃO
Nesta questão, precisamos analisar o gráfico e ver qual dos 3 fluidos consegue resfriar a peça até a temperatura de 100°C em menos de 8 segundos.
Observando o gráfico, percebemos que apenas os fluidos II e III conseguem resfriar a peça a 100°C, mas o fluido II demora 14 segundos para tal. Já o fluido III leva apenas 4 segundos.