01. Conhecimentos Numéricos
Questão 1
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
Espécie P : 4 anos no casulo ;
Espécie A: 8 anos no casulo;
Espécie B: 7 anos no casulo;
Espécie C: 6 anos no casulo;
Finalizando então, realizando um MMC (4,8) = 8 anos ;
MMC (4,7) = 28 anos ;
MMC (4,6) = 12 anos ;
Portanto, podemos ver que a primeira a ser ameaçada é a espécie A e a segunda que será ameaçada será a espécie C.
Questão 2
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
Temos que, na décima prestação, o valor devido é de 175 500. Calculando os juros, temos 1% de 175500 = 1755. Logo, na décima prestação o valor será de 1755 + 500 = 2255.
Questão 3
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Primeiro, sabemos que em 2010 o valor passou a ser R$360, um aumento de 20%, então qual era esse valor em 2009 antes dos 20%??
100%--------- X
120%--------- 360
120x = 36.000
x = 36.000/ 120
x = 300 ---> que é o valor da bolsa em 2009.
-Segundo, sabemos que ele concedia 29.000 mil bolsas em 2009, houve um aumento de 48% em 2010, qual esse aumento.
48/100 * 29.000
0,48 * 29.000 = 13.920 + 29.000 = 42.920 total de bolsas em 2010.
-Terceiro, encontrando valores em 2010:
42.920 bolsas------------A um valor de 360 reais === 15.451.200 reais gastos em bolsas.
Se fosse a um valor de 300 reais, seria um total de 12.876.000 reais.
Redução de 15.451.200 - 12.876.000 = 2.575.200 reais valor da redução.
-Quarto, com 2.575.200 reais quantas bolsas a mais seria possível??
Divide 2.575.200 pelo valor da bolsa (300).
2.575.200/ 300 = 8.584 número a mais de bolsas no lugar do aumento.
-Quinto, comparação.
29.000 mil bolsas em 2009
42.920 total de bolsas em 2010 + 8.584 número a mais de bolsas no lugar do aumento em 2010.
42.920 + 8.584 - 29.000.
51.000 - 29.000 = 22.504 número de bolsas que poderiam ser oferecidas em 2010.
Questão 4
GABARITO E RESOLUÇÃO
GABARITO E
RESOLUÇÃO
Vejamos as propostas que João tem à disposição:
a) renegociar as dívidas com o banco.
Caso João renegocie as dívidas (cheque e cartão) em 18 parcelas de R$ 125,00, ele pagaria 18 · 125 = R$ 2 250,00 (na renegociação parcelada do cheque + cartão)
b) pegar emprestado de José o dinheiro referente à quitação das duas dívidas.
Para quitar as duas dívidas de imediato, João precisaria tomar (cheque + cartão) 1500,00 + 300,00 = R$ 1800,00 de empréstimo e pagaria posteriormente ao amigo José 1800,00 + 25% · 1800,00 = 1800,00 · 1,25 = R$ 2 250,00 (o mesmo valor da proposta da alínea a)
c) recusar o empréstimo de José e pagar todas as parcelas pendentes nos devidos prazos.
Pagando as 12 parcelas do cheque e as 5 do cartão, nesta opção, João pagaria 12 · 150 + 5 · 800 = 1800 + 400 = R$ 2 200,00
d) pegar emprestado de José o dinheiro referente à quitação do cheque especial e pagar as parcelas do cartão de crédito.
Nesta opção, para quitar a dívida do cheque, João precisaria tomar emprestado R$ 1 500,00 e pagaria as 5 parcelas de R$ 80,00 referente à dívida do cartão, mais os juros de 25% sobre o valor que tomou de empréstimo com José:
1 500 · 1,25 + 5 · 80 = 1 875 + 400 = R$ 2 275,00.
e) pegar emprestado de José o dinheiro referente à quitação do cartão de crédito e pagar as parcelas do cheque especial.
Nesta opção, para quitar a dívida do cartão, João precisaria tomar emprestado R$ 300,00 e pagaria as 12 parcelas de R$ 150,00 referente à dívida do cheque, mais os juros de 25% sobre o valor que tomou de empréstimo com José:
300 · 1,25 + 12 · 150 = 375 + 1 800 = R$ 2 175,00
Questão 5
GABARITO E RESOLUÇÃO
GABARITO A
RESOLUÇÃO
A constante de proporcionalidade deve ser multiplicada pelas grandezas a que a resistência mecânica S é diretamente proporcional e dividida pelas grandezas inversamente proporcionais, o que dá a expressão da letra A.
Questão 6
GABARITO E RESOLUÇÃO
GABARITO A
RESOLUÇÃO
São necessários 14 milhões de quilogramas de banha para produzir 112 milhões de litros de biodiesel. Então, a regra de três será:
14 (banha) – 112 (biodiesel)
X (banha) – 48 (biodiesel)
112x = 672
x = 6
Questão 7
GABARITO E RESOLUÇÃO
GABARITO A
RESOLUÇÃO
Cada 5 ciclos de vênus são 8 anos na terra.
5 ciclos - 8 anos
x ciclos - 48 anos
8x = 240
x = 30 ciclos.
Questão 8
GABARITO E RESOLUÇÃO
GABARITO A
RESOLUÇÃO
A proporção recomendada da dosagem a cada 8 horas é de 5 gotas/2 kg de massa corporal (valor base) e a mãe ministrou corretamente 30 gotas a cada 8 horas.
Como a quantidade de gotas foi o sêxtuplo do valor base (5.6 = 30), seu filho tem o sêxtuplo de massa referente ao valor base (2 kg), 2.6 = 12 kg.
Questão 9
GABARITO E RESOLUÇÃO
GABARITO E
RESOLUÇÃO
Cada foto tem 2.0 megapixels, ou seja, dois milhões de pontos.
Já que as informações de cada ponto são armazenadas em 3 bytes, as informações de cada foto serão armazenadas em 2 milhões x 3 bytes = 6 milhões de bytes = 6 MB.
Como o algoritmo de compressão é de 95%, apenas 100% – 95% = 5% será utilizado, ou seja, 0,05 x 6 MB = 0,3 MB/foto. Logo, 0,3 MB x 150 = 45 MB para todas as 150 fotos.
O dispositivo que comporta esta capacidade e possui o menor espaço restante possível é o cartão de memória de 64 MB.
Questão 10
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Preço por kg da noz em cada supermercado é dado por:
A - > R$24,00
B - > R$3,00.4 = 12,00
C - > R$1,50.10 = 15,00
A sequência dos supermercados, de acordo com a ordem crescente do valor da noz, é B, C e A.
Questão 11
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Para determinar a taxa de fecundidade do ano 2020 primeiro temos que determinar a variação percentual do ano 2000, dividindo a taxa do período que queremos saber pelo total, e depois multiplicar esse valor percentual pelo valor de 2010. Da seguinte maneira:
1,9/2,38= t/1,9
2,38t = 3,61
t = 1,52
Questão 12
GABARITO E RESOLUÇÃO
GABARITO E
RESOLUÇÃO
Considerando que o anfitrião é um dos 30 convidados, para realizar a festa serão necessários:
– de carne, 250 g × 30 = 7 500 g = 7,5 kg
– de arroz, 1/4 de copo × 30 = 7,5 copos.
– de farofa, 4 colheres × 30 = 120 colheres.
– de vinho, 1/6 de garrafa × 30 = 5 garrafas.
– de cerveja, 1/2 de garrafa × 30 = 15 garrafas.
– de espumante, 1/3 de garrafa × 30 = 10 garrafas.
Questão 13
GABARITO E RESOLUÇÃO
GABARITO A
RESOLUÇÃO
M = 1000
C = 100
V = 5
XL = 50 – 10 = 40
I = 1
MCCV = 1205 * 1000 = 1.205.000
XLIII = 43 *1000 = 43.000
Questão 14
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
Analisando as informações, esta pessoa juntou R$95,05. Se ela dispõe de moedas de 1, 5, 10, 25 e 50 centavos, a cada 5 dias, junta-se R$0,91.
Agora, se dividirmos os R$95,05 por R$0,91, acharemos quantos grupos de 5 dias se formaram:
95,05/0,91=104+0,41
São 104 grupos de 5 dias, totalizando 520 dias. R$0,41 foram depositados nos últimos dias, começando pela moeda de 1 centavo.
R$0,41 equivale a soma de 1+5+10+25. Ou seja, a última moeda depositada foi a de 25 centavos no 524º dia.
Questão 15
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
As possibilidades de João efetuar as visitas são iguais a 5!⁄2= 120⁄2=60, que é o total de possibilidades descartando as simétricas. Como a questão fornece que João gasta 90 segundos (1min30) para cada sequência, logo, o tempo mínimo necessário é de 60x90 segundos=5400 segundos (90min).
Questão 16
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
Podemos visualizar que ele possui 4 opções de museus dentro do Brasil e deve escolher 3 e possui 4 opções de museu no exterior e deve escolher dois. A ordem em que ele visitará os museus não importa para sabermos o número de possibilidades.
Portanto devemos fazer uma análise combinatória para saber as possibilidades de combinação dentro do Brasil: 4 museus e 3 escolhas
C(4,3)= 4! / 3!*(4-3)!
= 4 . 3! / 3!*1!
= 4 / 1
= 4 maneiras para escolher os 3 museus no Brasil.
E depois uma para as possibilidades no exterior: 4 museus e duas escolhas
C(4,2)= 4! / 2!*(4-2)!
= 4 . 3 . 2! / 2!*2!
= 12 / 2
= 6 maneiras para escolher os 2 museus no exterior.
E então, multiplicamos os dois resultados (4x6) e obtemos o resultado final, 24 combinações diferentes.
Questão 17
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Calcula-se a quantidade de água por hora que consegue ser eliminada por cada ralo pelos dados fornecidos do reservatório que a indústria já possui. São 900m³ de água para seis ralos, assim 900 : 6 = 150m³ por ralo em seis horas, 150 : 6 = 25m³ por hora por ralo. Os ralos são idênticos e devem esvaziar o novo reservatório em quatro horas, logo cada um eliminará 25 x 4 = 100m³ de água. Como a capacidade do novo reservatório é de 500m, serão necessários 500 : 100 = 5 ralos.
Questão 18
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
O lucro médio de cada empresa será:
F: 24 ÷ 3 = 8 milhões de reais
G: 24 ÷ 2 = 12 milhões de reais
H: 25 ÷ 2,5 = 10 milhões de reais
M: 15 ÷ 1,5 = 10 milhões de reais
P: 9 ÷ 1,5 = 6 milhões de reais
A empresa que apresenta o maior lucro anual é a empresa G.
Questão 19
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
Deverá ser escolhida a marca de pão que apresenta a maior razão entre a massa de fibras e a massa de pão. Calculando as concentrações de fibras em cada uma das marcas, temos:
A: 2/50 = 0,040
B: 5/40 = 0,125
C: 5/100 = 0,050
D: 6/90 ≈ 0,067
E: 7/70 = 0,100
Assim, deverá ser escolhida a marca B.
Questão 20
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
A receita no segundo dia será 4 ⋅ 16 + 40 + 0,2 ⋅ 40 = 112 reais e o valor de venda de cada picolé deve ser 112 / (20 ⋅ 4) = R$ 1,40
Questão 21
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Volume Total = 5 . 800 mL = 4000 mL
4 horas ——- 0,4 . 4000 mL = 1600 mL
Faltam 4000 – 1600 = 2400 mL
Como 1 mL = 12 gotas
2400 mL = y
y = 28.800 gotas
Então, o número de gotas/minuto restante será: 28800 / 20.60 = 24 gotas/min
Questão 22
GABARITO E RESOLUÇÃO
GABARITO A
RESOLUÇÃO
Bairro I -> 14/400 = 3,5%
Bairro II -> 6/500 = 1,2%
Bairro III -> 13/520 = 2,5%
Bairro IV -> 9/360 = 2,5%
Bairro V -> 15/500 = 3%
Logo, o bairro I apresentou o maior índice.
Questão 23
GABARITO E RESOLUÇÃO
GABARITO E
RESOLUÇÃO
Como a área do evento é de 500² m² e a cada m² cabem 4 pessoas, às 10 horas da manhã havia 4 ⋅ 500² = 1 000 000 de pessoas presentes e até as 4 horas da tarde chegarão mais 120 000 ⋅ 6 = 720 00 pessoas.
Assim serão necessários 1 720 000/2 000 = 860 policiais.
Questão 24
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Sempre que precisarmos comparar frações, devemos colocá-las no mesmo denominador.
Colocaremos todas no denominador 8.
½ = 4/8
⅜
5/4 = 10/8
Como podemos ver, ⅜ < 4/8 < 10/8
Ou seja, ⅜ < ½ < 5/4.
Questão 25
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Tempo do Sonic Wind LSRV para percorrer 1 000 km a 3 000 km/h:
3 000 km ____ 1h = 60 min
1 000 km ____ x min
x = 20 minutos.
Tempo do Concorde para percorrer 1 000 km a 2 330 km/h:
2 330 km ____ 60min
1 000 km ____ y min
y = 25.75 minutos
Resposta = y – x = 25.75 – 20 = 5,75, aproximadamente 6.
Questão 26
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
A variação da pena é de 12 a 48 meses, só que devemos analisar esta variação para um funcionário público, que tem aumento de ⅓ da pena.
12 + ⅓.12 = 16
48 + ⅓.48 = 64
Ou seja, a pena, para um funcionário público, varia de 16 a 64 meses.
Questão 27
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
A menor despesa é R$10,80 (3 de 100g) + R$10,00 = R$20,80
Questão 28
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
Calculando o MMC (2,3,4) = 12 descobre-se o intervalo entre eles baterem palmas simultaneamente. Sabendo que as palmas iniciaram em 1 segundo com intervalo de repetição de 12 segundos, pode construir uma P.A.: (1,13,25,37,49). Apenas com n entre 1 e 5 pois o n=6 passaria de 60 segundos. A lei de formação da PA: an=1+ (n-1).12
Questão 29
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
O menor custo será dado por:
Subir no elevador 1= 0,15
Descer no elevador 1= 0,10
Subir no elevador 2= 1,80
Descer no elevador 2= 2,30
Cujo custo será de R$4,35.
Questão 30
GABARITO E RESOLUÇÃO
GABARITO E
RESOLUÇÃO
O número de colorações possíveis, com no máximo 4 cores, é 4 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 972;
Questão 31
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
Como sabemos que o seu último termo que é 61,50 toneladas, para saber a quantidade total será necessário empregar a fórmula da soma dos termos de uma P.A que é representada por:
Sn = (a₁ + an).n/2
sendo:
n= 10 termos
Ficaremos com a seguinte expressão:
S₁₀ = (a₁ + a₁₀).10/2
S₁₀ = (50,25 + 61,50).5
S₁₀ = (111,75).5
S₁₀ = 558,75 toneladas
Questão 32
GABARITO E RESOLUÇÃO
GABARITO A
RESOLUÇÃO
=> Situação Inicial
Temos 10 algarismos para ocupar 6 dígitos, sem restrições donde resultam 10 possibilidades para cada dígito
Logo o número (N) de senhas inicial seria:
N = 10.10.10.10.10.10 = 10^6
=> Situação Final
--> Temos 10 algarismos
--> Temos 26 letras minúsculas
--> Temos 26 letras Maiúsculas
Continuamos a ter 6 dígitos para preencher mas note que desta vez temos 62 possibilidades para cada dígito, as 10 que já tínhamos inicialmente mais 52 da alteração de segurança (26 maiúsculas + 26 minúsculas)
Assim as possibilidades das novas senhas são:
N = 62.62.62.62.62.62 = 62^6
Donde resulta o coeficiente de melhoria (Cm):
Cm = Situação atual/Situação inicial
Cm = 62^6/10^6
Questão 33
GABARITO E RESOLUÇÃO
GABARITO E
RESOLUÇÃO
Temos que o número N = 2x.5y.7z. Assim, temos que o número de divisores de N é (x+1).(y+1).(z+1), incluindo o próprio N.
Como queremos os divisores diferentes de N, teremos: (x+1).(y+1).(z+1) – 1.
Questão 34
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
O aumento é proporcional ao que o vendedor conseguiu aumentar nas vendas. Se o vendedor vendesse R$600,00 ele receberia R$120,00, mas se vendesse R$1.200,00 ele receberia R$200,00, ou seja, não é proporcional. Sendo assim, repare que ao aumentar em R$600,00 as vendas, ele receberia R$80,00 a mais. Sendo assim, como o funcionário vendeu R$990,00, ele aumentou as vendas em R$390,00. Agora sim podemos usar uma regra de três
600 – 80
390 – X
600X = 31.200
X = 52
Sendo assim, o funcionário receberá os 120 iniciais, mais X = 52, pelo o que conseguiu aumentar nas vendas. Total R$172,00.
Questão 35
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
Fazendo o total de pessoas, temos 4,5 + 2 + 2,5 + 0,5 + 20,5 = 3. Fazendo o total de pessoas vacinadas, temos: 0,9 + 1 + 1,5 + 0,4 + 8,2 = 12. Fazendo a porcentagem, temos 12/30 = 0,4 = 40%.
Questão 36
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
De acordo com os dados na tabela, vemos que, de 2014 até 2015, houve uma redução de 50 acidentes. Ou seja, em 1 ano houve um decrescimento de 50. Precisamos calcular a variação referente a 4 anos, de 2014 até 2018.
Assim, podemos fazer uma regra de 3:
1 ano – 50
4 anos – x
X = 200
Ou seja, em 2018, o número de acidentes foi de 900 – 200 = 700.
Questão 37
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
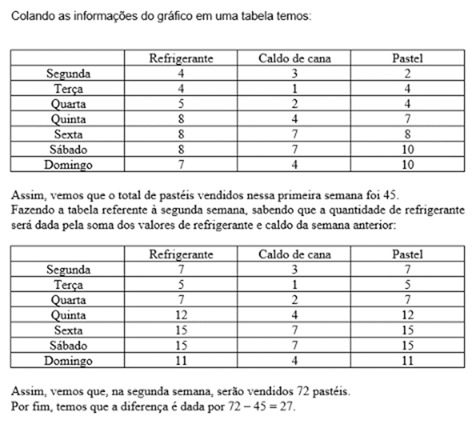
Questão 38
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Como 0 < x < 1, teremos uma função exponencial decrescente.
y = x^e
Quanto menor o valor de “e”, maior será o valor de y. Com isso x^(1/3).
Questão 39
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO

Questão 40
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO

Questão 41
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
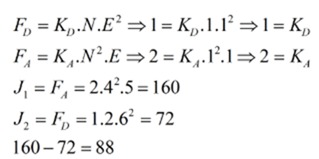
Questão 42
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
Pacientes que não foram curados com o tratamento tradicional: 100%-40% = 60%
Pacientes curados pelo primeiro tratamento: 1/2 . 60% .35% = 1/2 . 0,6 . 0,35 =0,105 = 10,5%.
Pacientes curados pelo segundo tratamento: 1/2 . 60% .45% = 1/2 . 0,6 .0,45 = 0,135 = 13,5%
Em relação ao total de pacientes submetidos inicialmente, os tratamentos inovadores proporcionaram cura de: 10,5% + 13,5% = 24%
Questão 43
GABARITO E RESOLUÇÃO
GABARITO E
RESOLUÇÃO
63 kWh --------- 100%
A redução no consumo implica em menos 20%, ou o consumo passará a ser apenas 80% do anterior.
63kWh ------------ 100%
x 80%
100x = 63 . 80 ------- 100x = 5040 ------- x = 5040/100 ------ x = 50,4 kWh
Aproximando teremos 50 kWh.
Questão 44
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
As cartas organizadas nas colunas formam uma PA de razão 1, (1,2,3,4,5,6,7). A soma desta PA pode ser calculada segundo a fórmula, sendo an o termo que ocupa a última posição e n o total de termos da PA.
Neste caso o monte é formado pelas cartas que sobraram 52 – 28 = 24.
Questão 45
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
Primeiro, precisamos calcular o total de períodos (n) que precisam ser jogados para que a criança obtenha os 9 200 tíquetes.
Como ela ganha 20 por período jogado, e cada período jogado custa 3 reais, o total gasto é de 460 x 3 = 1380 reais.
Questão 46
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Como o time B não ficou entre os três últimos colocados, concluiu-se que B ocupou uma das primeiras posições. Como a posição do time A superou a posição do time C, C superou a posição do time E, e D superou a posição do time A, concluímos que D também ocupa uma das duas primeiras posições.
Portanto, os times que possuem a melhor classificação são B e D.
Questão 47
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
É fácil ver que o número de quadrados pretos que restam após a n-ésima iteração é dado por 8n.
Portanto, após a terceira iteração, o número de quadrados pretos que restam é igual a 8³ = 512.
Questão 48
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
O lucro do contribuinte será: L = 34 000 – 26 000 = 8 000 reais
O Imposto de Renda que esse contribuinte terá que pagar será: 15% . L =0,15 . 8 000= 1 200
Questão 49
GABARITO E RESOLUÇÃO
GABARITO E
RESOLUÇÃO
Para o pacote 1, o preço a ser pagos por x shows assistidos é:
P1(x) = 40x
Para o pacote 2, o preço a ser pagos por x shows assistidos é:
P2(x) = 80 + 10x
Para o pacote 3, o preço a ser pagos por x shows assistidos é:
P3(x) = 60 + 15(x - 4)
Como João assistirá 7 shows, temos que nos pacotes ele pagaria:
P1(7) = 40.7 = R$280
P2(7) = 80 + 10.7 = R$150
P3(7) = 60 + 15(7 - 4) = R$107
Como Maria assistirá 4 shows, temos que nos pacotes ela pagaria:
P1(4) = 40.4 = R$160
P2(4) = 80 + 10.4 = R$120
P3(4) = 60 + 15(4 - 4) = R$60
A melhor opção para ambos é o pacote 3.
Questão 50
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
Com 1 kWh, a diferença entre gasto dos consumidores de consumo mensal 185 kWh e 100 kWh é, em reais:
85,56/185 – 16,73/100 ≅ 0,46 – 0,17 = 0,29
Questão 51
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Pelo enunciado, o tempo de digitação em cada tentativa é de 30 s. Aplicando o conceito de progressão geométrica no cálculo do tempo de espera entre as digitações, é possível construir a seguinte tabela com o registro do tempo gasto, em segundos, pela pessoa na ativação do rádio.
O tempo total será dado pela soma dos registros, que é igual a 30 + 60 + 30 + 120 + 30 + 240 + 30 = 540 segundos.
Questão 52
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
Se M = R$ 400,00 é o montante desejado e n é o número mínimo de meses necessário, então
400 = 200 (1 + 0,05)n (1,05)n = 2
log (1,05)n = log2
n.log(1,05) = log2
n = 0,3/0,02
n = 15
Questão 53
GABARITO E RESOLUÇÃO
GABARITO A
RESOLUÇÃO
O ideal seria de 6 gramas de sal por dia, o que indica 2,4 gramas de sódio ao dia.
Para chegar a essa conclusão use que o sal de cozinha é composto por 40% de sódio e 60% de cloro ao longo de 30 dias a pessoa consumiu 450 gramas de sal:
quanto é 40% de 450 gramas?
100% ----- 450 gramas.
40% ------- X gramas.
100x = 450. 40
100x = 18000
x = 18000 ÷ 100
x = 180 gramas de sódio durante 30 dias.
180g --------- 100%
x g----------------40%
40. 180 = 100x
7200 = 100x
x = 7200 ÷ 100
x = 72 gramas de sódio seria o ideal
72 g--- 100%
180 g ---- X%
72x = 180. 100
72x = 18000
x = 250
250 - 100
= 150% de excesso
Questão 54
GABARITO E RESOLUÇÃO
GABARITO E
RESOLUÇÃO
Além das ligações locais para fixos, o valor gasto com as ligações para celulares foi de 200 - 40 = R$160. A assinatura mensal foi descontada pois dá direito apenas para ligação para fixos.
Para que a conta telefônica dê R$80, as ligações para celular devem ser de 80 - 40 = R$40. Ou seja, descontada a assinatura mensal, a ligação para celulares deve passar de R$160 para R$40.
Em percentual, supondo que a relação entre preço e quantidade de ligações é diretamente proporcional, temos:
%ligações = 40 / 160 = 0,25 = 25%
Logo, a redução percentual dos gastos em ligações para celulares deve ser de:
%redução = 100% - %ligações
%redução = 100 - 25
%redução = 75%
Questão 55
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
Para começarmos, 106 é igual ao número 1 seguido de seis zeros. Então:
106 = 1 000 000
Para calcular 6,7 × 106, basta multiplicarmos 6,7 por 1 000 000.
6,7 x 1 000 000 = 6 700 000
1000 é um milhar
10 000 é uma dezena de milhar
100 000 é uma centena de milhar
700 000 são 7 centenas de milhar
Questão 56
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
A produção atual é dada pelo produto entre produtividade e área, conforme:
Pinicial = 40 x 2,5 + 100 x 1 = 220
A produção desejada é 15% maior que a produção atual, pelo acréscimo de terras de produtividade igual a 1. Ou seja:
Pdesejada = 40 x 2,5 + (100 + x) x 1 = 1,15 x 220
Logo, a área a ser adquirida é de:
X = 33
Questão 57
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
São n parcelas cada uma no valor de x reais. Logo, o valor total é nx. Segundo o enunciado, temos:
(n + 5)(x – 200) = nx
(n – a)(x + 232) = nx
Da primeira equação, temos nx – 200n + 5x – 1000 = nx. Assi, 5x – 200n = 1000. Ou seja x – 40n = 200.
Da segunda equação, temos: nx + 232n – 4x – 928 = nx. Assim, 232n – 4x = 928. Ou seja, 58n – x = 232.
Assim, temos duas equações e duas incógnitas, que nos dão um sistema. Resolvendo o sistema, encontramos n = 18 e x = 24.
Questão 58
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
Sendo x a capacidade máxima do caminhão, temos que cada saco de cimento ocupa x/60 da capacidade máxima, cada saco de cal ocupa x/90 e cada lata de areia ocupa x/120.
O pedido de 15 sacos de cimento e 30 sacos de cal ocupa um total de:
Capacidade ocupada: 15.(x/60) + 30.(x/90) = x/4 + x/3 = 7x/12
A capacidade restante do caminhão é:
x - 7x/12 = 5x/12
Dividindo a capacidade restante pela ocupação das latas de areia, temos:
(5x/12)/(x/120) = 5x.120/12x = 50 latas
Questão 59
GABARITO E RESOLUÇÃO
GABARITO E
RESOLUÇÃO
Calculando em metros a distância percorrida em 8 voltas pelo carro B:
ΔS = V * Δt
onde,
ΔS: distância percorrida;
V: velocidade, no caso, 14 m/s;
Δt: variação de tempo, no caso, 288 segundos.
Aos cálculos:
ΔS = V * Δt
ΔS = 14 * 288
ΔS = 4032 m
Logo, se 8 voltas tem o valor de 4032 metros, 10 voltas terá:
x = (4032 / 8) * 10
x = 5040 metros
Calculando agora o tempo em que o carro A completou a 10 voltas:
ΔS = V * Δt
5040 = 18 * Δt
Δt = 5040 / 18
Δt = 280 segundos
Finalmente calculando a distância, em metro, que o carro B percorreu do início da corrida até o momento em que o carro A completou a décima volta foi mais:
ΔS = V * Δt
ΔS = 14 * 280
ΔS = 3920 metros
Questão 60
GABARITO E RESOLUÇÃO
GABARITO C
RESOLUÇÃO
A questão da a informação de que a foto foi enviada em uma escala 1:5, ou seja para cada um centímetro na imagem corresponde a 5 centímetros reais.
É dada a informação de que o artista recebeu a imagem da escala e imprimiu ela em papel de forma 3 vezes ampliada, sendo assim o vaso ficou com um total de 30 cm, dessa forma dividindo 30 cm, por 3 teremos o tamanho do vaso na imagem original.
30 cm / 3 = 10 cm.
Sabemos então que 10 cm é a altura do vaso na imagem e que é usada uma escala de 1:5, sendo assim teremos que:
10 cm x 5 = 50 cm
Questão 61
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
>O preço do café é R$ 400,00 em uma saca de 60 Kg.
> Depois de perder umidade o preço do café passa a ser R$ 400,00 em uma saca de 50 kg.
Como o café será vendido em embalagens de 1kg o preço de cada embalagem pode ser obtido por meio de uma regra de três simples sendo que:
R$ 400.............50 Kg
X R$...................1 Kg
x= 400/50
x = R$ 8,00
Como o torrefador quer obter um lucro de 200% em relação ao valor pago durante a compra ele precisa somar R$ 16,00 ao valor inicial pois:
200% de 8 => 200/100 * 8 => 16
Assim temos que o valor do café será R$ 8,00 (valor inicial) + R$ 16,00 (valor do lucro) obtendo um total de R$ 24,00 por unidade.
Questão 62
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
Do enunciado, temos:
Área total a ser pintada: 260 m²;
Área que o pintor faz em 8 horas: 40 m²;
Preço por dia do pintor: R$240,00;
Orçamento total do cliente: R$4600,00;
Para pintar 260 m², o pintor gasta:
d = 260/40 = 6,5 dias
O valor cobrado nesses 6,5 dias será:
c = 6 . 240 + 0,5 . 240
c = R$1560,00
Dividindo o orçamento pelo valor acima:
x = 4600/1560
x = 2,95
Portanto, as paredes serão pintadas no máximo duas vezes.
Questão 63
GABARITO E RESOLUÇÃO
GABARITO B
RESOLUÇÃO
Para cada mão de tinta na casa inteira o pintor precisará de 260/40 = 6,5 dias de oito horas ou 6 dias e 4 horas. Logo, a despesa com uma mão de tinta é 6.240 + 120 = R$ 1.560,00.
Em consequência, com o orçamento do cliente, será possível dar 4600/1560 = 2 mãos de tinta.
Questão 64
GABARITO E RESOLUÇÃO
GABARITO D
RESOLUÇÃO
Olhando o gráfico, no segmento GH a força aplicada é a maior.